문제 : https://www.acmicpc.net/problem/5977
5977번: Mowing the Lawn
FJ has 5 cows whose efficiencies are 1, 2, 3, 4, and 5, in that order. He wants to choose some of the cows such that their total efficiency is maximized, but he cannot choose more than 2 consecutive cows. FJ chooses all cows but the third. The total effici
www.acmicpc.net
문제 파악하기
N 마리의 소 중, 연속된 번호의 소를 K마리보다 많이 선택하지 않으면서 효율성이 최대가 되게 만드는 경우를 구하는 문제입니다. 모든 소는 1번부터 연속된 번호를 부여받으며, 각각의 소가 가지고 있는 효율성이 제시됩니다. 소는 최대 100,000마리가 주어질 수 있기에 O(N2)보다 빠른 알고리즘이 필요하며, 각각의 소는 최대 1,000,000,000의 효율성을 가질 수 있기에 int형이 아닌 long long int형을 사용해야 한다는 점을 알 수 있습니다. 이 점을 명심하며 문제를 해결할 알고리즘을 설계해봅시다.
우선, 어떤 소를 골라야 할지 생각해봅시다. 선택할 소를 고르는 건 생각할 요소가 좀 많습니다. 지금 확인할 소를 선택할 수 있는지 여부도 확인해야 하며, 현재 소를 골랐을 때의 효율성까지 고민해야 합니다. 그렇기에 초점을 바꿔봅시다. 선택할 소가 아닌, 제외할 소를 골라봅시다. 제외할 소는 일정 범위(범위<=K+1) 안에서만 선택하면 되기에 훨씬 쉽게 문제가 바뀝니다. 하지만 단순히 재귀함수를 사용하기에는 시간이 오래 걸리기 때문에 좀 더 효율적인 알고리즘이 필요합니다.
문제 해결하기
제외할 소를 고르는 알고리즘은 다음과 같은 점화식을 만들 수 있습니다.
dp[ i ] = min( dp[ i-1 ] ~ dp[ i-K-1 ] ) ( dp[ i ]: i번째 소를 제외할 때의 최솟값 )
여기서 최솟값을 구하는 이유는 선택할 소의 최댓값을 구하기 위해서이며, 범위가 (i-K-1) ~ (i-1)로 정해져있는 이유는 소는 최대 K마리를 연속해서 선택할 수 있기 때문입니다. 여기서 우리는 세그먼트 트리를 사용할 수도 있지만 데큐를 사용하면 좀 더 효율적으로 문제를 해결할 수 있습니다. 데큐란 데이터의 삽입/산출이 양 끝단(front, rear)에서 일어날 수 있는 큐를 의미하며, 특수한 상황에서 점화식을 효과적으로 처리할 수 있습니다.
데큐를 사용할 수 있는 상황은 데큐 안에 단조함수, 즉 오름차순 혹은 내림차순으로 값을 저장할 수 있을 때 입니다. 그리고 이번 문제는 다행히 데큐 안에 오름차순으로 값을 저장할 수 있습니다. 만약 ( i < j ) 이며, ( dp[ i ] > dp[ j ] )인 값이 있다고 가정해봅시다. 그럼 우리는 탐색 시 dp[ i ]의 값은 볼 필요가 없습니다. dp[ i ]보다 작으면서 더 멀리 있는 값인 dp[ j ]값만 신경쓰면 됩니다. 이는 우리가 할 탐색이 더 가까이 있는 값이 더 나중의 값에 영향을 미칠 수 있으며, 더 작은 값이 더 효율적인 탐색이기 때문입니다. 아래 그림을 보며 좀 더 생각해봅시다.
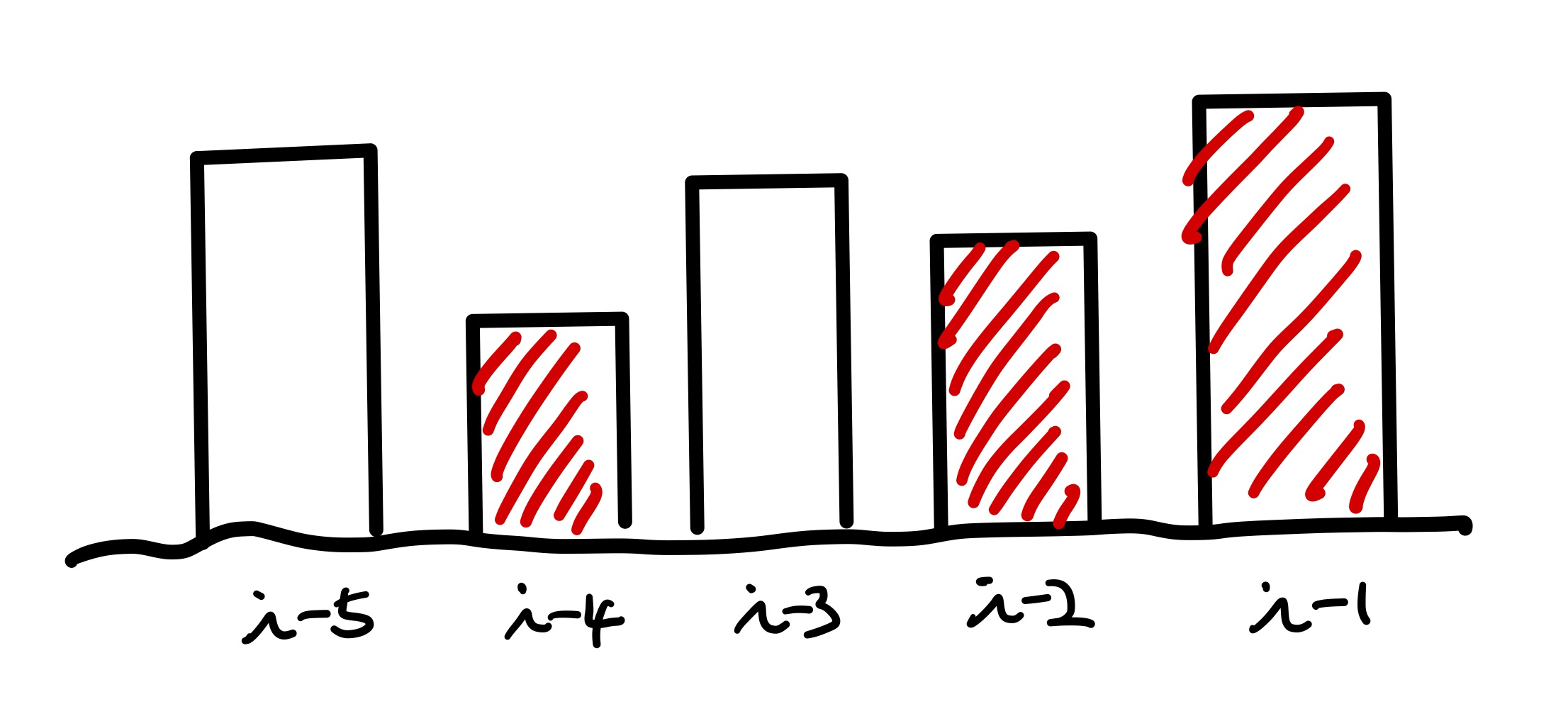
그림의 사각형을 각각의 소를 제거했을 때, 제거되는 효율성이라고 하겠습니다. 위의 5개의 값 중에서 신경쓰지 않아도 되는 값이 있습니다. 바로 dp[ i-5 ]와 dp[ i-3 ] 값입니다. 두 값 모두 dp[ i ]한테 좀 더 가까이 있으면서 작은 값들이 있습니다. 따라서, 위의 빨간색으로 색칠한 값을 제외하고는 데큐에서 제외하면 됩니다. 그러면 데큐에는 항상 오름차순으로 값을 저장할 수 있으며, 맨 앞(front)에는 가장 작은 값이 저장되게 됩니다. 이렇게 데큐 안의 값을 오름차순으로 유지하면서 dp[ i ]의 값을 채우면 우리는 원하는 정답을 구할 수 있습니다.
데큐에 값을 활용한 알고리즘은 다음과 같습니다.
( 1 ) i로 이동할 수 없는 값을 데큐에서 제거한다. ( i-K-1이 나오기 전까지 제거 )
( 2 ) dp[ i ]의 값 구하기 >> dp[ i ] = dq.front( ) + inp[ i ]
( 3 ) dp[ i ]의 값을 데큐에 적절한 위치에 넣기 >> dq.back( )을 확인하고 pop_back( )하면서 오름차순 유지
( 4 ) i가 N-K 이상이라면 값 확인하기( N-K부터 탐색 종료 가능 )
dp[ i ]의 값은 최솟값을 더해야하며, 데큐 안에서 최솟값은 항상 맨 앞(front)에 위치합니다. 그리고 만약 현재 값( dp[ i ] )보다 큰 값이 데큐에 들어있다면 제거해주면서 데큐 값을 정리해주면 됩니다. 그리고 i가 N-K가 되었다면 나머지 값은 모두 선택한다는 가정 하에 탐색을 종료할 수 있습니다. 따라서, ( dp[ N-K ] ~ dp[ N ] )까지의 최솟값을 구해주면 우리가 원하는 결괏값을 얻을 수 있습니다.
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
#include <stdio.h>
#include <deque>
#define NMAX 100010
#define INF 1e14
#define lint long long int
using namespace std;
int N, K;
lint inp[NMAX];
lint tot, ret;
lint dp[NMAX];
deque< int > dq;
int main() {
// 입력
scanf("%d %d", &N, &K);
for(int i=1;i<=N;i++) {
scanf("%lld", &inp[i]);
tot += inp[i];
}
// 제외할 소 선택하기 >> dp[i]: i번 소를 제외할 때의 최솟값
ret = INF;
dq.push_back(0);
for(int i=1;i<=N;i++) {
// (K+1) 이내의 소를 제외할 수 있음 >> 범위를 넘어가는 경우 제외
while(!dq.empty()) {
if( (i-dq.front()) <= K+1 ) break;
dq.pop_front();
}
// dp[i] 값 >> dp[(i-K-1):(i-1)] 중 만들 수 있는 가장 작은 값(dq.front())
// N-K 부터는 모든 소를 포함시킬 수 있음 >> 탐색 종료 가능
dp[i] = dp[dq.front()] + inp[i];
if(i >= N-K) ret = min( ret, dp[i] );
// 데큐 안의 값 정리 >> 오름차순
while(!dq.empty()) {
if(dp[i] > dp[dq.back()]) break;
dq.pop_back();
}
dq.push_back(i);
}
printf("%lld", tot-ret);
}
/*
8 2
5 0 1 0 1 5 5 1
ans: 16
*/
|
cs |
후기
데큐를 사용한 동적 프로그래밍을 처음 풀어보아서 조금 헤맸지만 나름 신선한 아이디어에 재미있던 문제였습니다. 역시 USACO 문제라고 생각하며, 동적 프로그래밍 혹은 LIS를 심화하고 싶은 사람에게 추천하고 싶은 문제입니다.
'문제 노트 > 백준' 카테고리의 다른 글
| 복구( BOJ 15908 ) (0) | 2022.08.12 |
|---|---|
| 변신 이동 게임( BOJ 15906 ) (0) | 2022.08.09 |
| Ignition( BOJ 13141 ) (0) | 2022.08.01 |
| 임계경로( BOJ 1948 ) (0) | 2022.07.31 |
| 보석 모으기( BOJ 1480 ) (0) | 2022.07.30 |